Design Decision
Database System을 설계할 때 크게 고려해야 할 점은 `Data Organizaiton`와 `Concurrency`이다.
Data Organizaiton
효율적인 접근을 위해 memory/page에 어떻게 data structure를 배치할 것인지, 그리고 어떤 정보를 저장할 것인지에 대한 문제이다.
Concurrency
어던 방식으로 multiple thread가 data structure에 문제를 발생시키지 않으면서 동시에 접근하게 할 수 있는지를 고려하는 문제이다.
Hash Table
Hash Table은 key와 value를 mapping하는 unordered associative array를 implements한다.
`Hash function`을 사용해서 주어진 키에 대해 array에서의 offset을 계산하고, 원하는 value를 도출해낸다.
공간 복잡도는 `O(n)`이며
시간 복잡도는 Average `O(1)`이고 Worst `O(n)`이다.
Worst case는 변환된 hash 값이 충돌이 발생하는 `Hash Collision`에 해당하며, Hash Collision 발생 시 `Chaining`이나 `Open Addressing` 방식으로 처리하게되는데, 하나의 엔트리에 모든 target이 배정되는 경우 O(n) time이 된다.
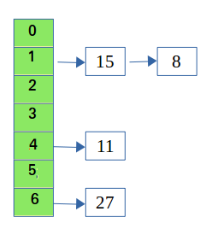
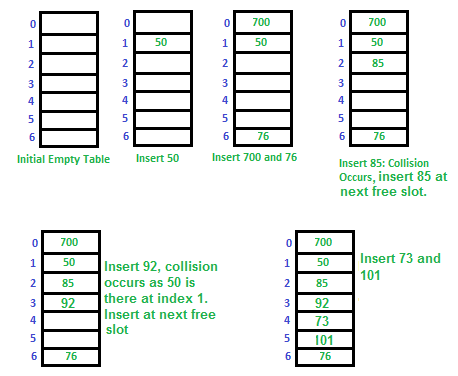
Static Hash Table
고정크기의 배열을 이용하여 데이터를 저장하는 방식에 해당한다.
entry를 찾기 위해서 hash된 값을 배열의 크기로 나눈 나머지로 얻은 offset을 활용한다.
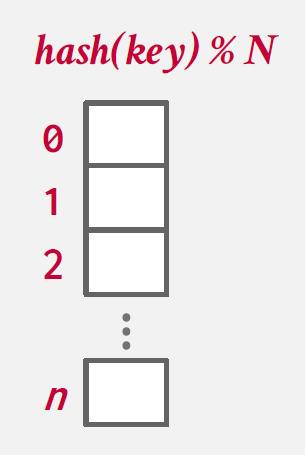
다만 Static Hash Table은 몇 가지 현실적이지 않은 가정을 바탕으로 설계되어있다.
1. Number of elements is known ahead of time and fixed
해시테이블을 사용하기 전에 저장할 요소의 개수를 정확히 알아야하며, 이 개수가 고정되어 있다는 가정이다.
다만 실제로는 데이터의 양이나 크기가 변하는 경우가 흔하기때문에 이러한 가정은 현실적이지않다.
2. Each key is unique
모든 key가 고유하다는 것을 가정한다. 하지만 실제로는 중복된 키가 발행될 수 있으며, 이를 처리하는 방법을 고려해야한다.
3. Perfect hash function guarantees no collisions
완벽한 해시 함수를 사용하여 충돌이 발생하지 않는다는 것을 가정한다.
즉 Static Hash Table은 실제 상황에서 효율적으로 사용되기에는 많은 한계점이 있으며, 우리는 Hash Table을 설계할 때 다음과 같은 부분들을 고려해야 한다.
1. Hash Function
해시 함수의 설게에는 속도와 충돌률간의 trade-off가 존재한다.
2. Hashing Scheme
해시 스키마는 Hash Collision 발생 시 어떻게 처리할지에 대한 구조를 말한다.
큰 해시테이블을 할당하는 방법과 추가적인 명령어를 사용하여 키를 삽입하고 검색하는 방법(Chaining, Open Address)으로 나뉘며, 이는 해시 테이블의 메모리 사용량과 성능에 영향을 미친다.
Hash Functions
어떠한 key에 대해서, 해당 key를 표현하는 interger를 리턴해주는 함수를 말한다.
즉 입력 key를 이용하여 해시 테이블의 인덱스로 사용할 수 있다.
DBMS에서의 해시 테이블을 위한 해시 함수로는 암호학적인 해시 함수들(ex. SHA-2)를 사용하지 않는다.
DBMS의 해시 테이블은 보안 요구 사항이 아니라 빠르고 hash collision이 적은 해시 함수가 필요하기 때문이다.
DBMS 해시 테이블에서 원하는 해시 함수의 특성은 빠르고, collision이 낮다는 점이다.
여기서 빠르다는 것은 key를 정수로 변환하는데 걸리는 시간을 의미하며, collision이 낮다는 것은 서로 다른 입력키를 동일한 hash 값으로 매핑시키는 경우가 적다는 것을 의미한다.
Static Hashing Schemes
Linear Probe Hashing
선형 탐색 해싱은 Hash Collision이 발생한 경우, 다음 가능한 해시 위치로 선형적으로 이동하여 비어있는 슬롯을 찾는 방식으로, `Open Address` 방식의 처리방법에 해당한다.
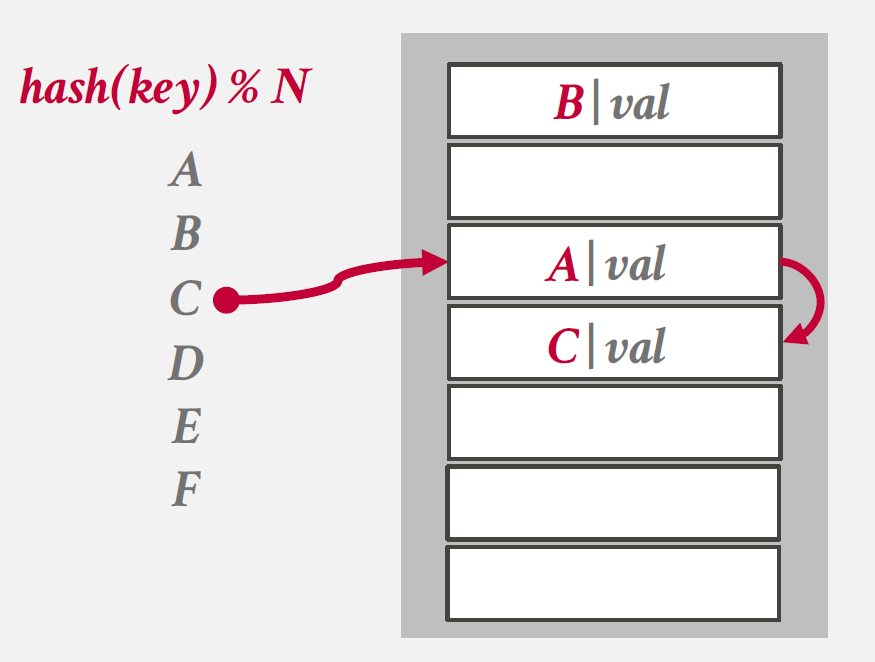
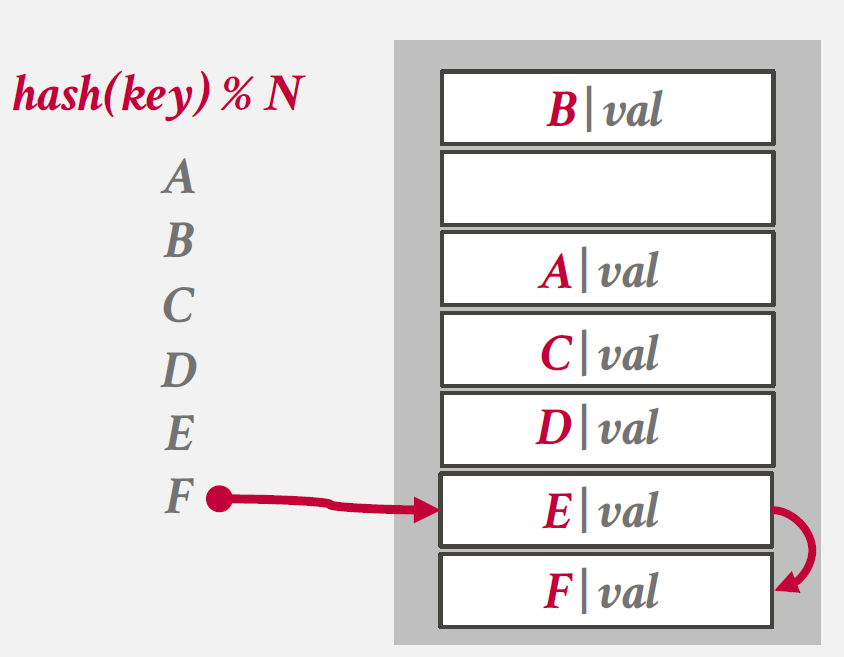
그림을 살펴보면, C를 hashing한 이후 A와의 collision이 발생하여 A 다음 entry에 C를 할당하는 것을 확인할 수 있다.
이러한 Linear Hasing 방식에서 Delete가 발생할 경우 `Tombstone` 방식으로 처리할 수 있다.
이는 삭제 요청에 대해 실제로 삭제하는 것이 아닌, Tombstone이라고 marking한 후, 후속 요청을 처리하는 것을 의미한다.
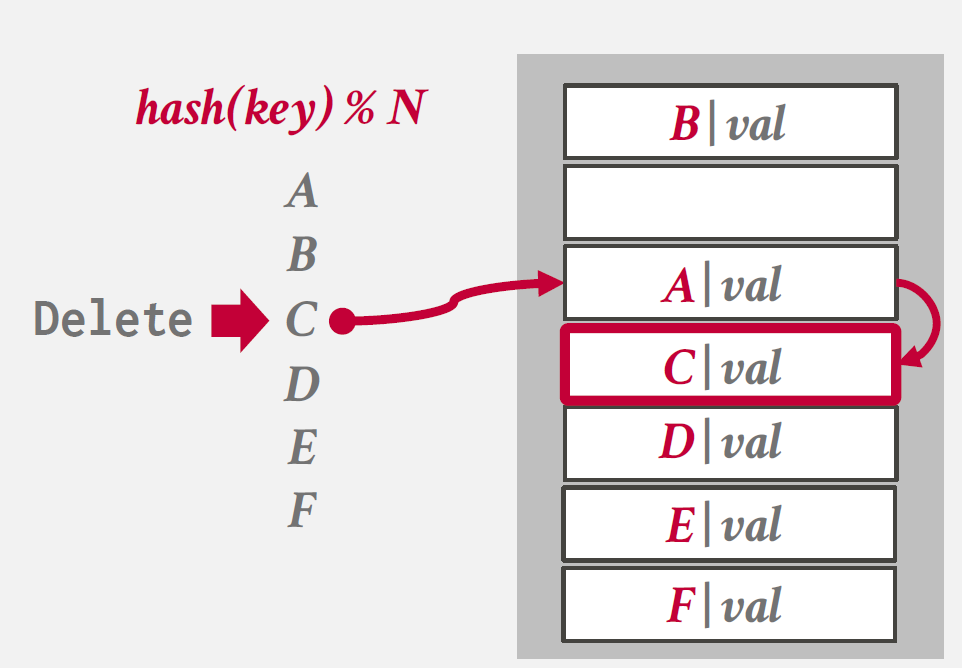
C에 대한 Delete 요청이 들어오면, C의 key를 사용하여 Hash를 진행한다.
이후 A와 Hash Collision이 발생했었기 때문에 해당 위치에는 C가 아닌 다른 정보가 들어있고, 따라서 이후 Linear Probe를 진행한다.
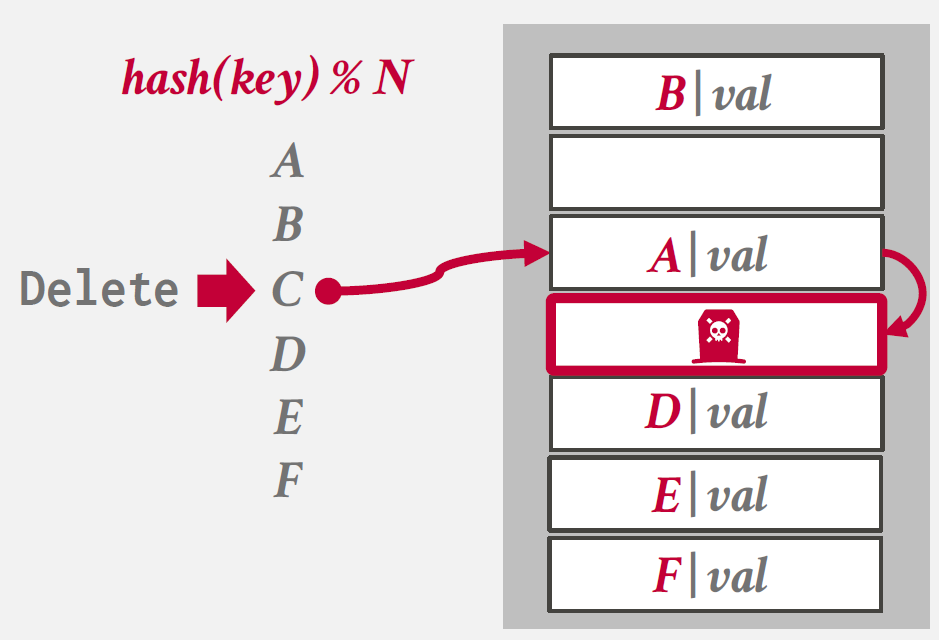
C를 담고 있는 entry를 만나면, 논리적인 삭제 동작을 진행하여 Tombstone marking을 진행한다.

이후 TombStone에 대한 hash collision이 발생하는 요청이 들어올 경우, Linear Probe를 통해 일치하는 entry가 이미 존재하는지 확인한다.
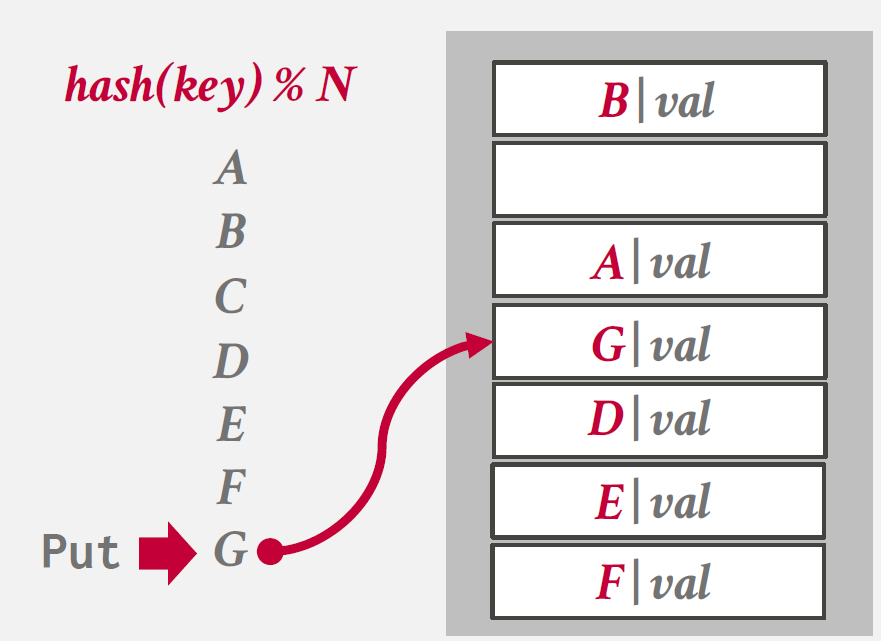
만약 새로운 정보가 입력될 경우 Tombstone marking을 제거하고 요청을 처리한다.
Cuckoo Hashing
records를 insert하기 위해 hash functions를 여러개 사용하여 hash table의 multiple locations를 찾아내는 방식을 말한다.
Insert시, 여러 hash functions를 사용해 multiple locations에 접근하고 비어있는 하나의 entry를 선택한다.
만약 빈 공간이 존재하지 않으면 하나의 element를 evict하여 다른 location을 찾기 위한 re-hash를 진행한다.
Insert 과정을 나타낸 그림을 아래와 같다.
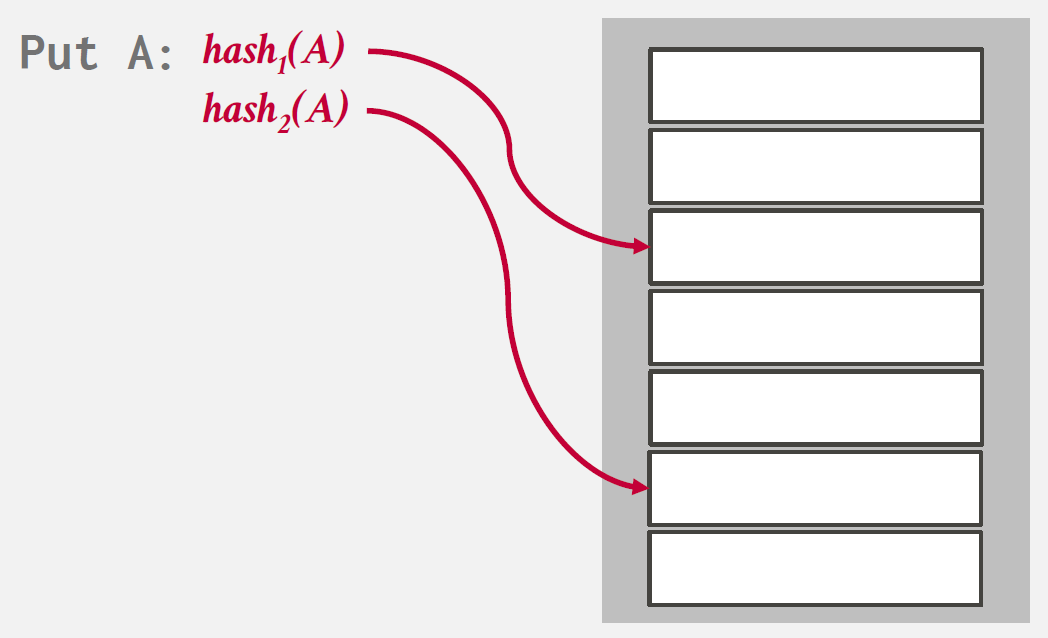
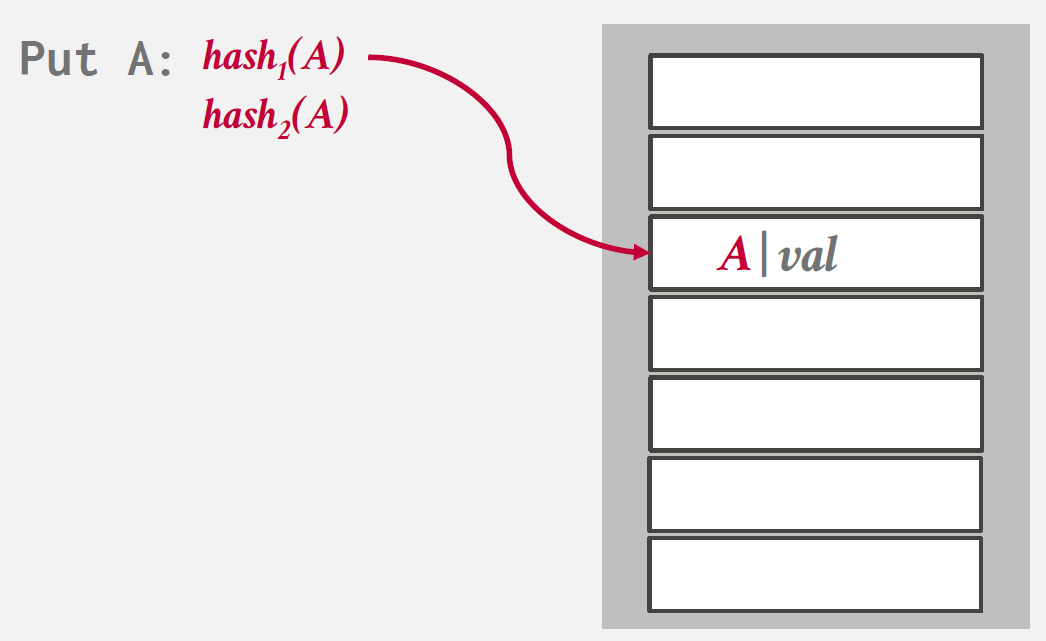

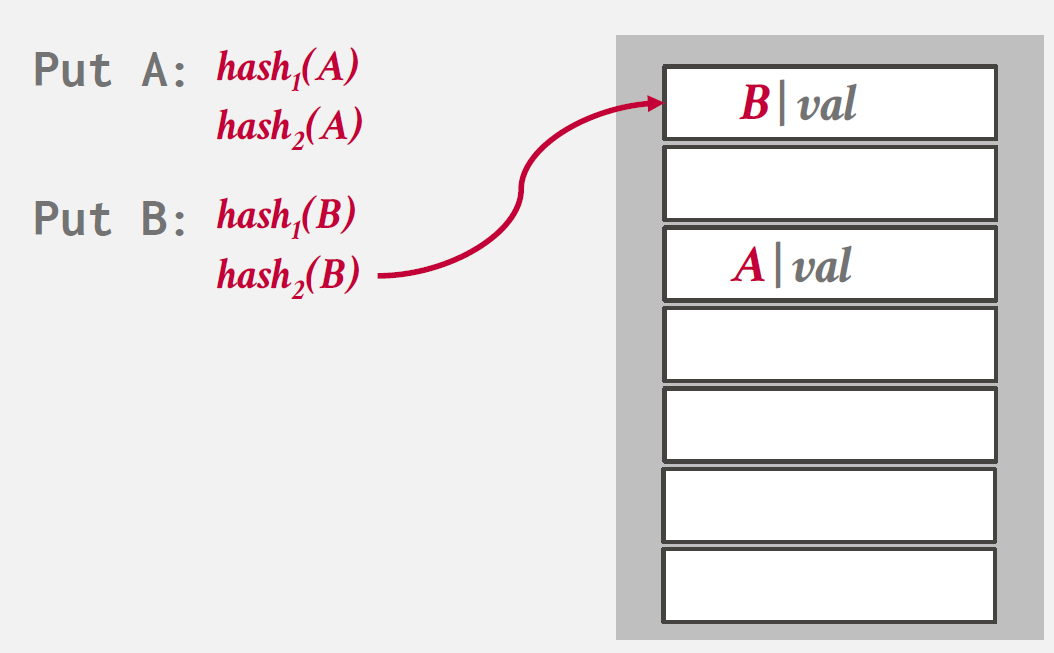
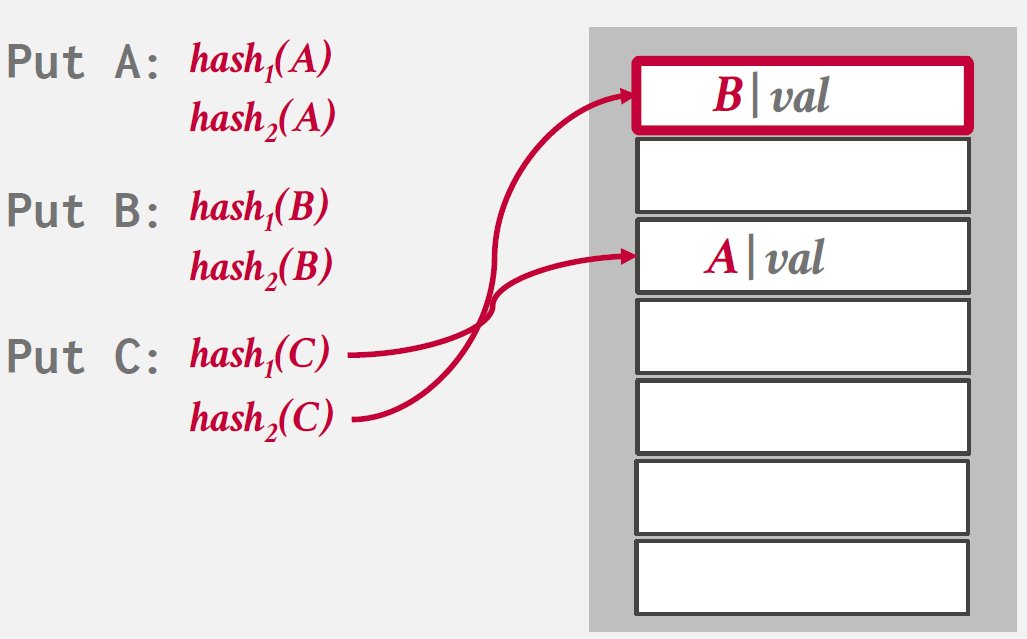
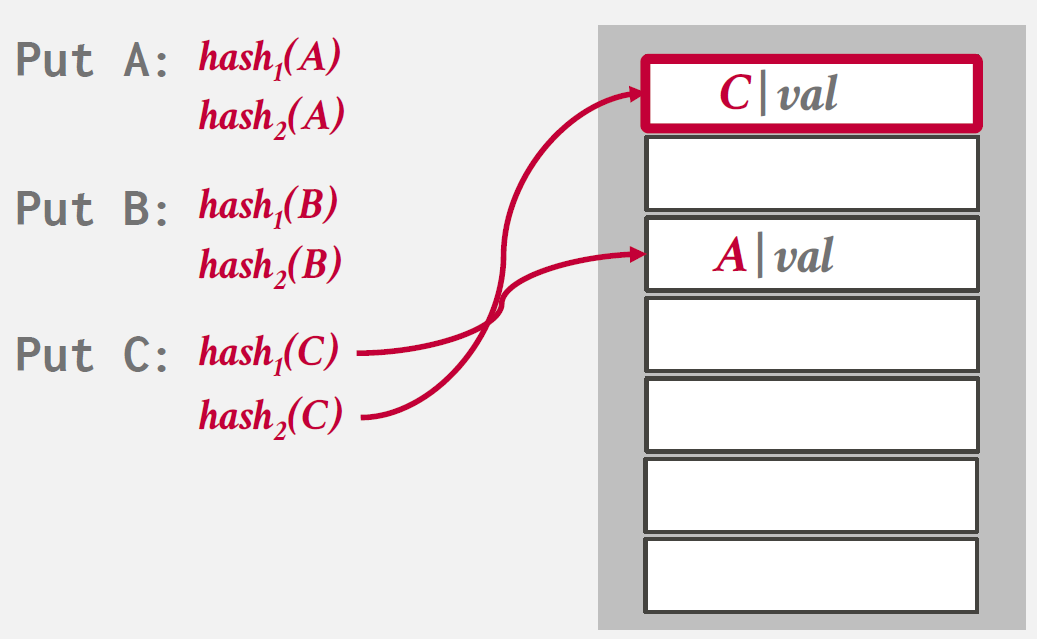
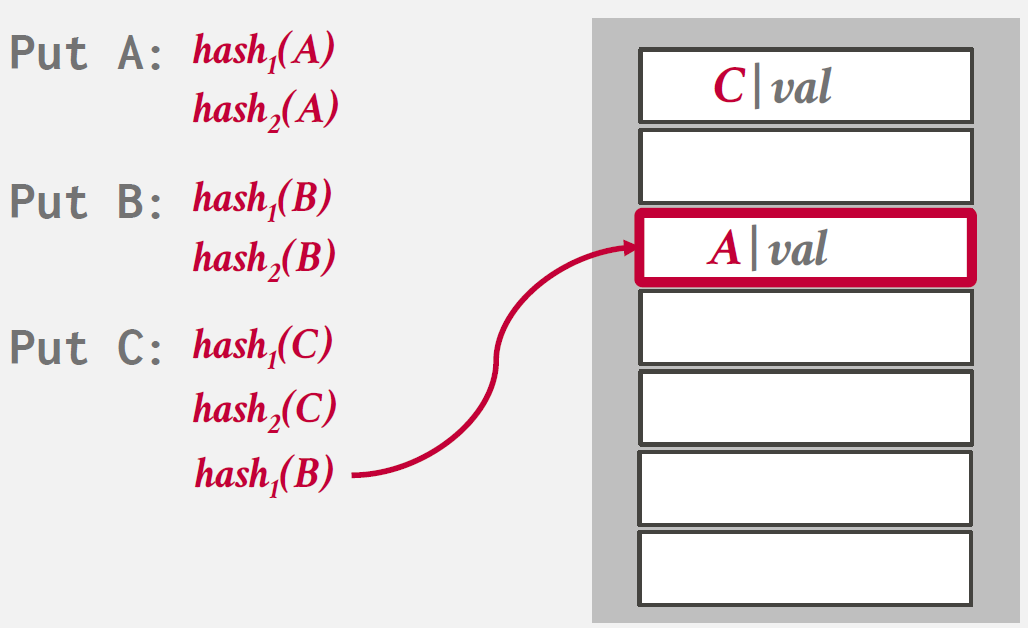
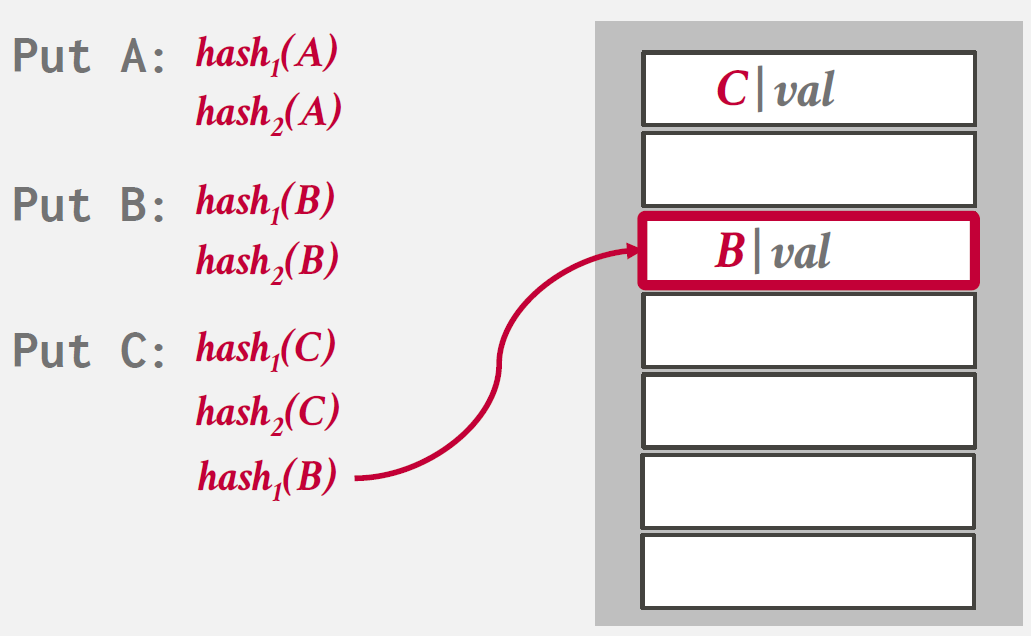
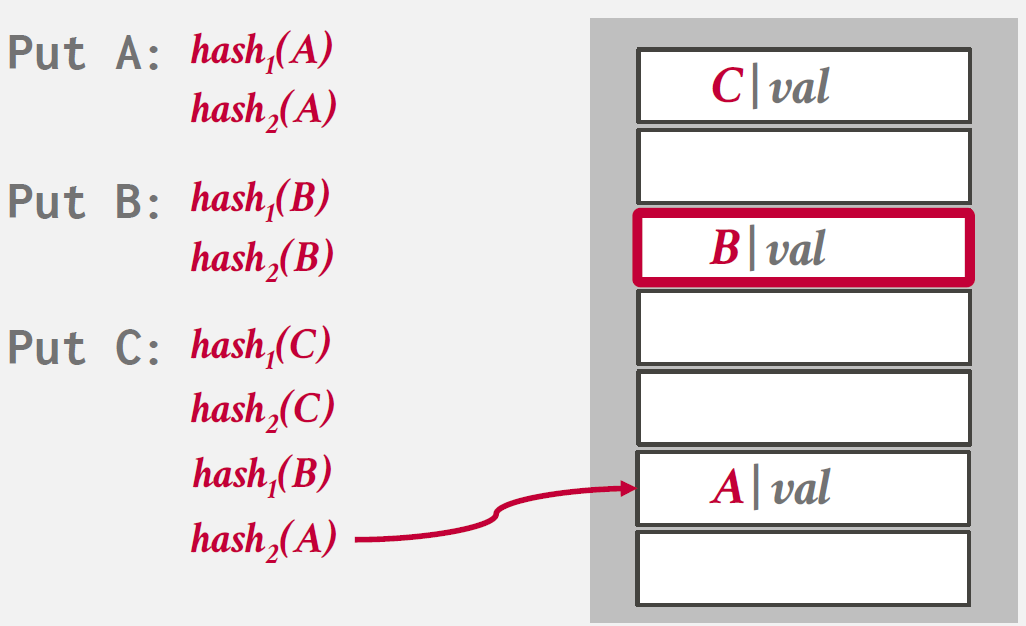
Non-Unique Keys
해시 테이블에서 중복되는 키를 다루는 방법에는 크게 두 가지 옵션이 존재한다.
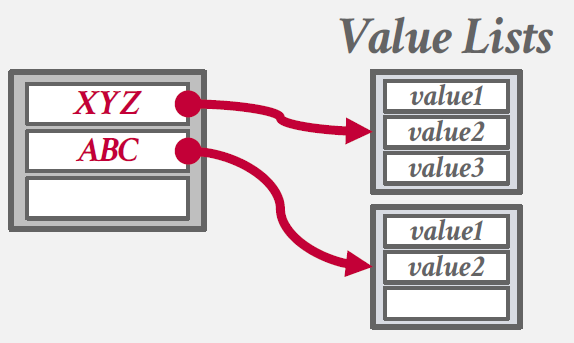
Seperate Linked List
중복되는 키에 대한 값을 별도의 Linked List에 저장하는 방법이다.
즉 동일한 Hash 값을 가지는 여러 key-value 쌍을 동일한 슬롯에 저장하지 않고, 각 키에 대한 값들을 별도의 Linked List로 구성한다.
확장이 자유롭다는 장점이 있으나, 중복된 키가 많은 경우 성능적인 측면에서 문제가 발생할 수 있다.
Redundant Keys
중복되는 key-value 쌍을 해시 테이블 내에서 중복 키를 허용하면서 저장하는 방법이다.
대부분의 시스템에서 사용하는 방식으로, 중복된 키를 효과적으로 처리할 수 있다.
동일한 슬롯 내에 중복 키값을 저장하기 때문에 검색이 빠르고 효율적이며, 중복 키를 허용하기 때문에 중복 여부를 확ㅇ니하는 추가적인 연산이 필요하지 않기 때문이다.
중복 키가 많아지면 슬롯 내에서의 데이터 관리 및 검색의 복잡성이 증가할 수 있다는 단점이 있다.

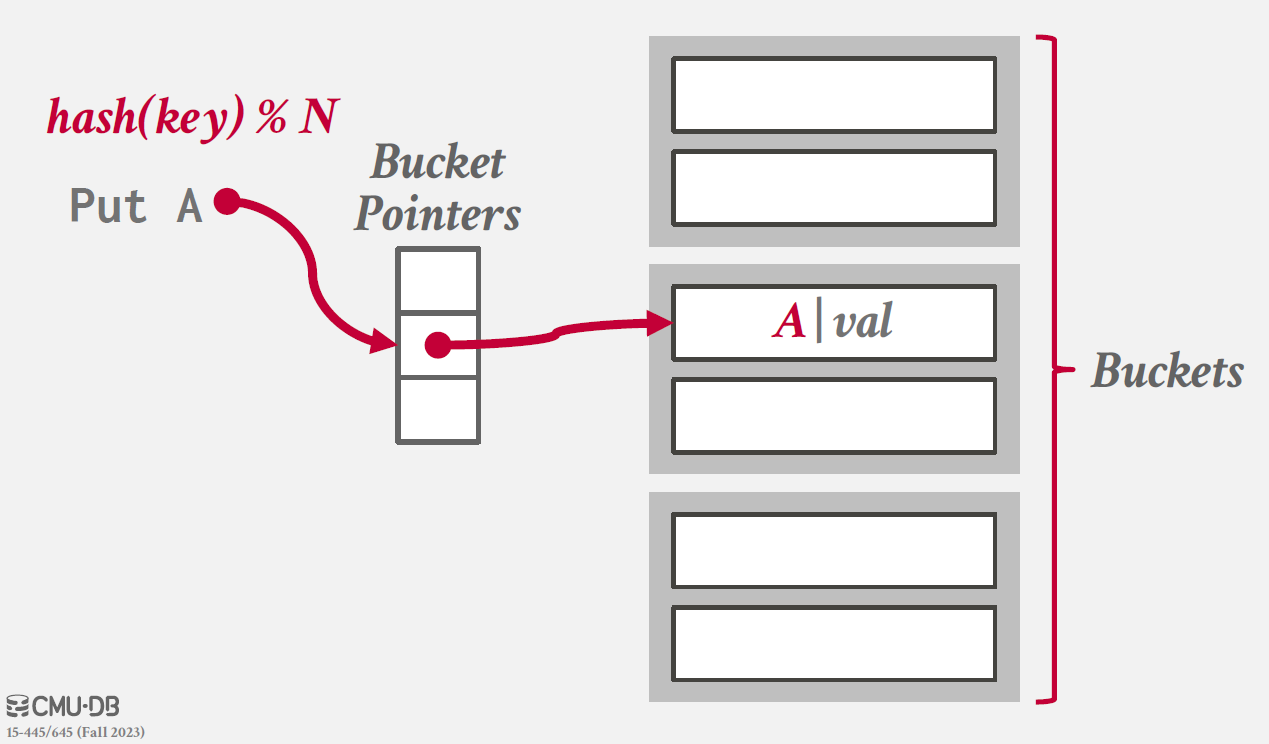
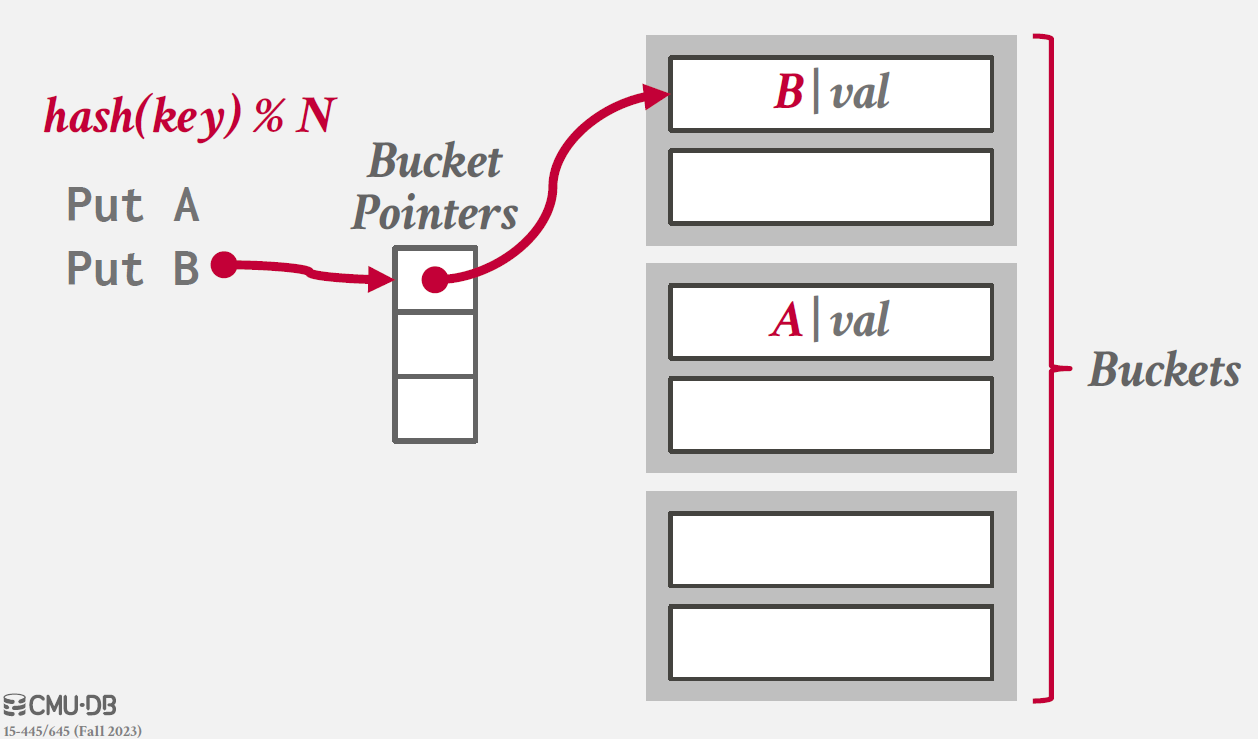
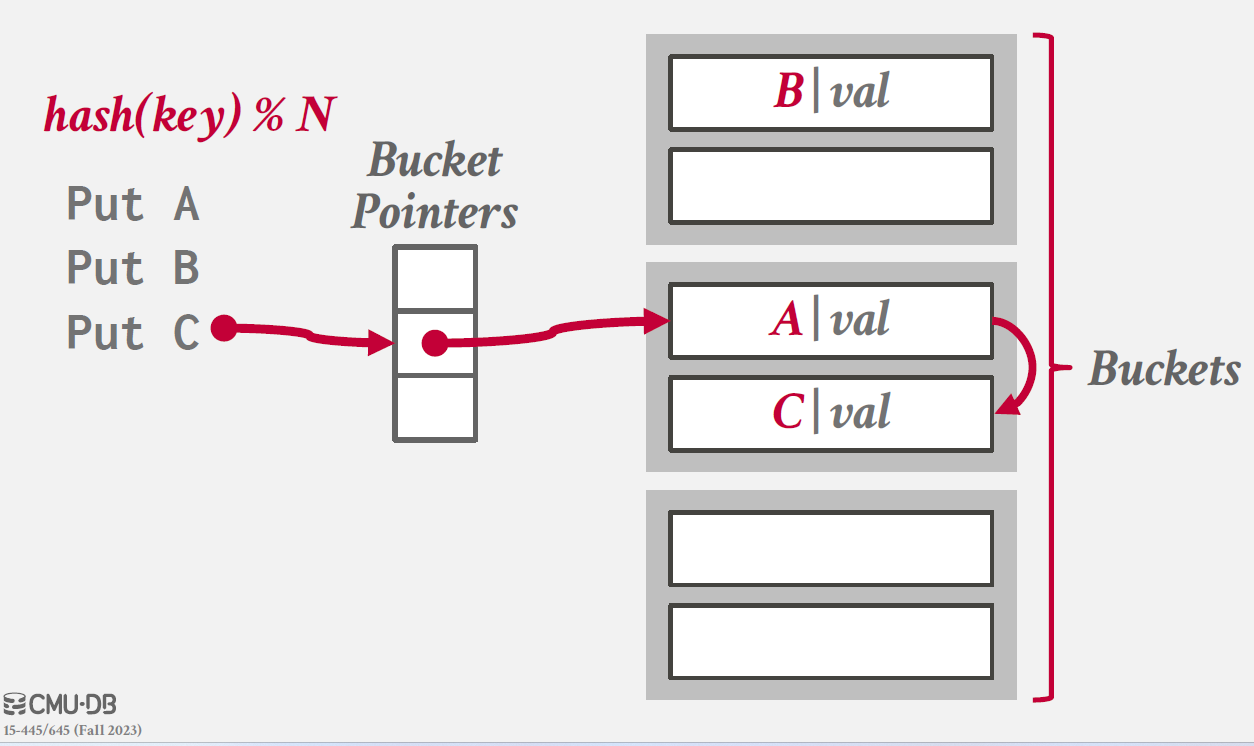
Chained Hashing
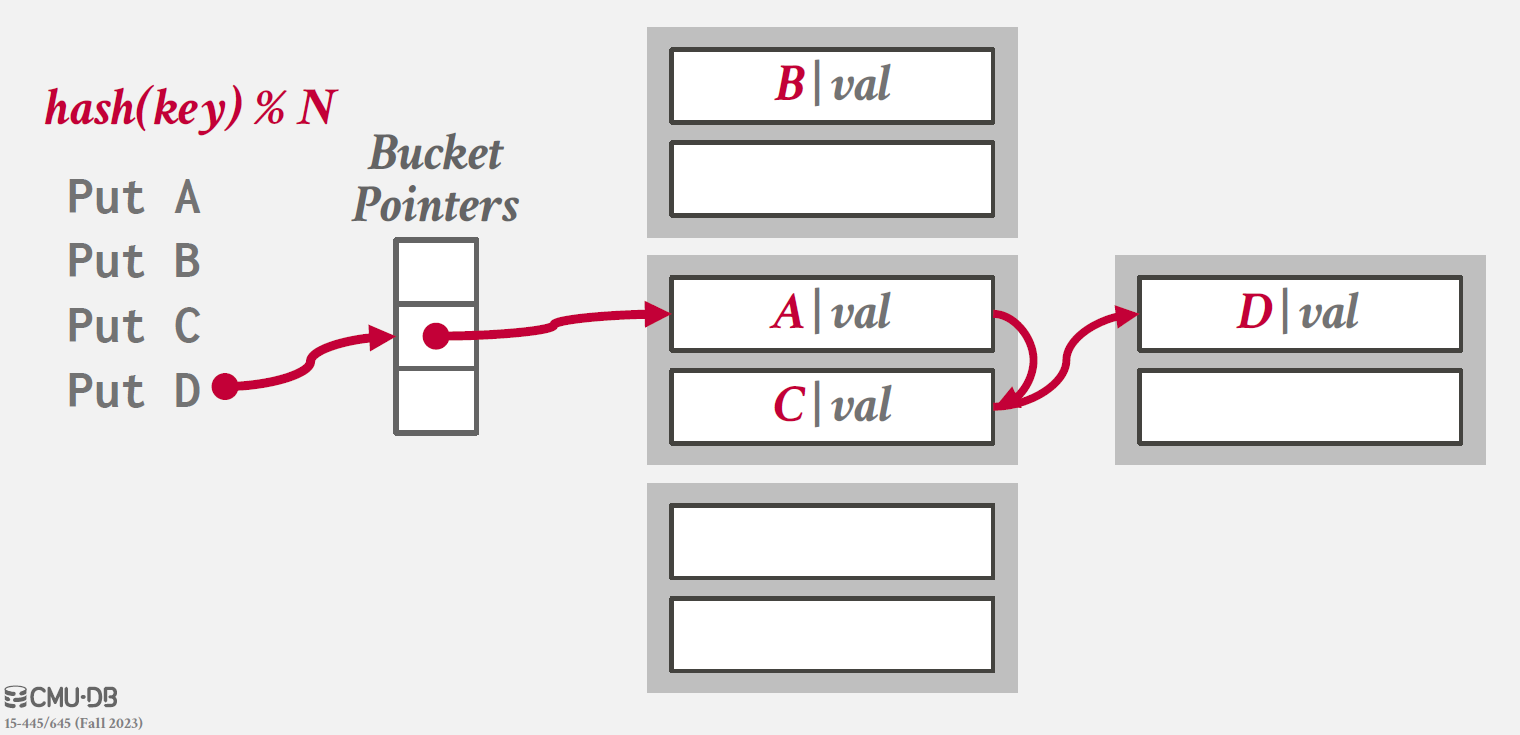
hash table의 각 slot에 대햇 linked list of `buckets`를 운영하는 방식이다.
같은 key를 가지는 elements들을 같은 bucket에 넣으면서 collision 문제를 해결한다.
동작 방식은 아래와 같다.
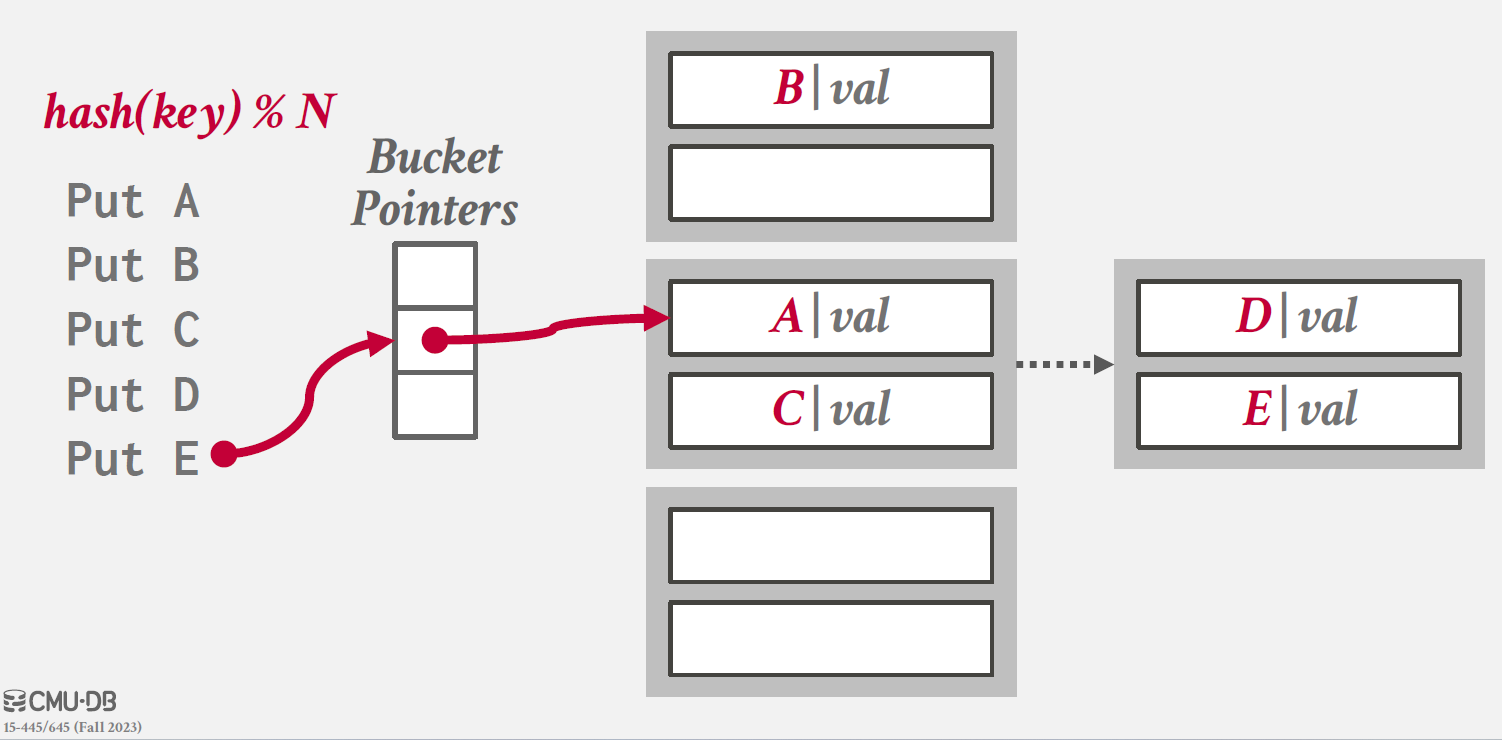
Linear Hashing
overflow가 발생하여 더 이상 해당 bucket에 값을 insert할 수 없을 때, pointer가 추적하고 있는 bucket을 split하여 공간을 확보하는 방식이다.
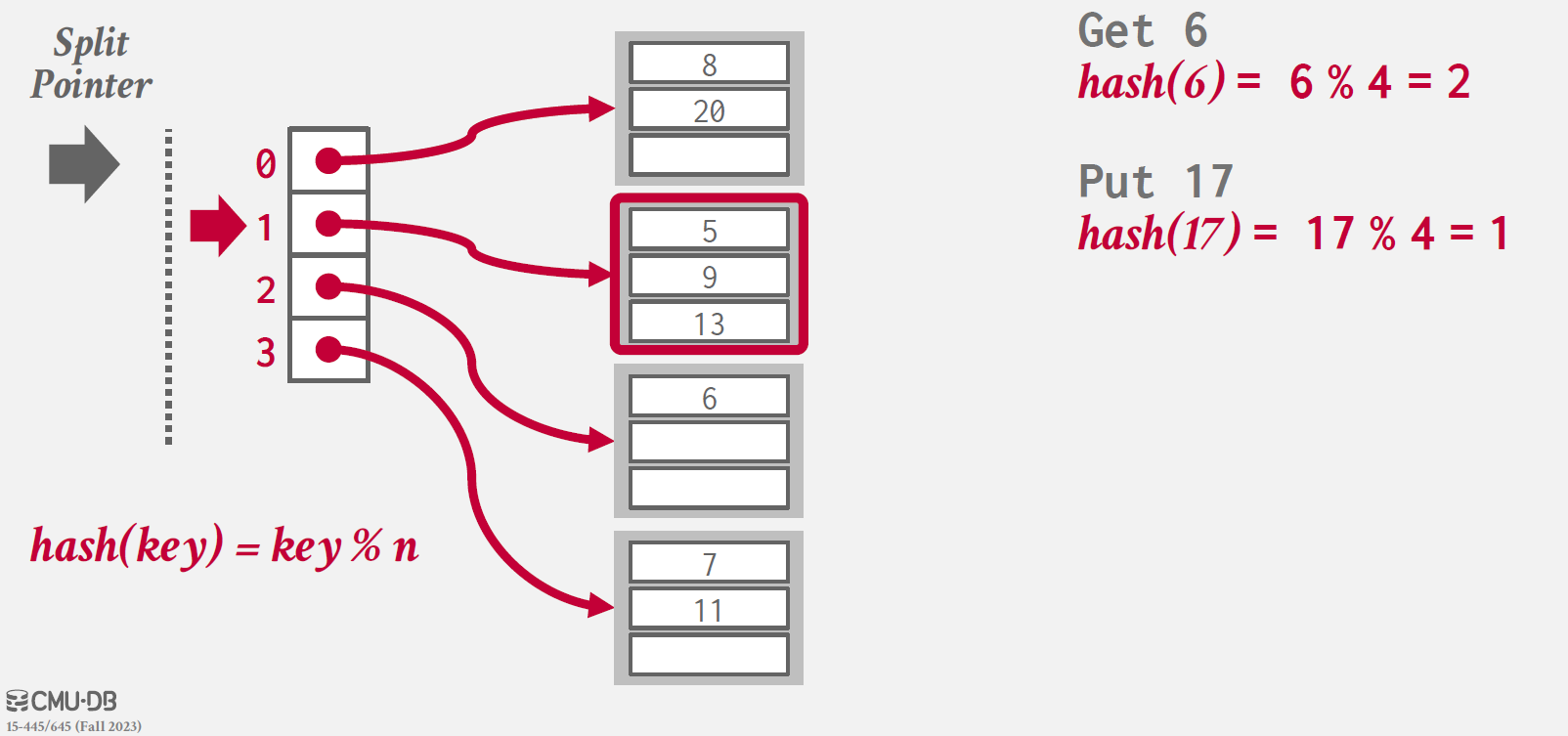
위와 같이, 17을 PUT하려는데 index 1 값을 가진 bucket이 가득 차 있기 때문에, overflow가 발생한다.
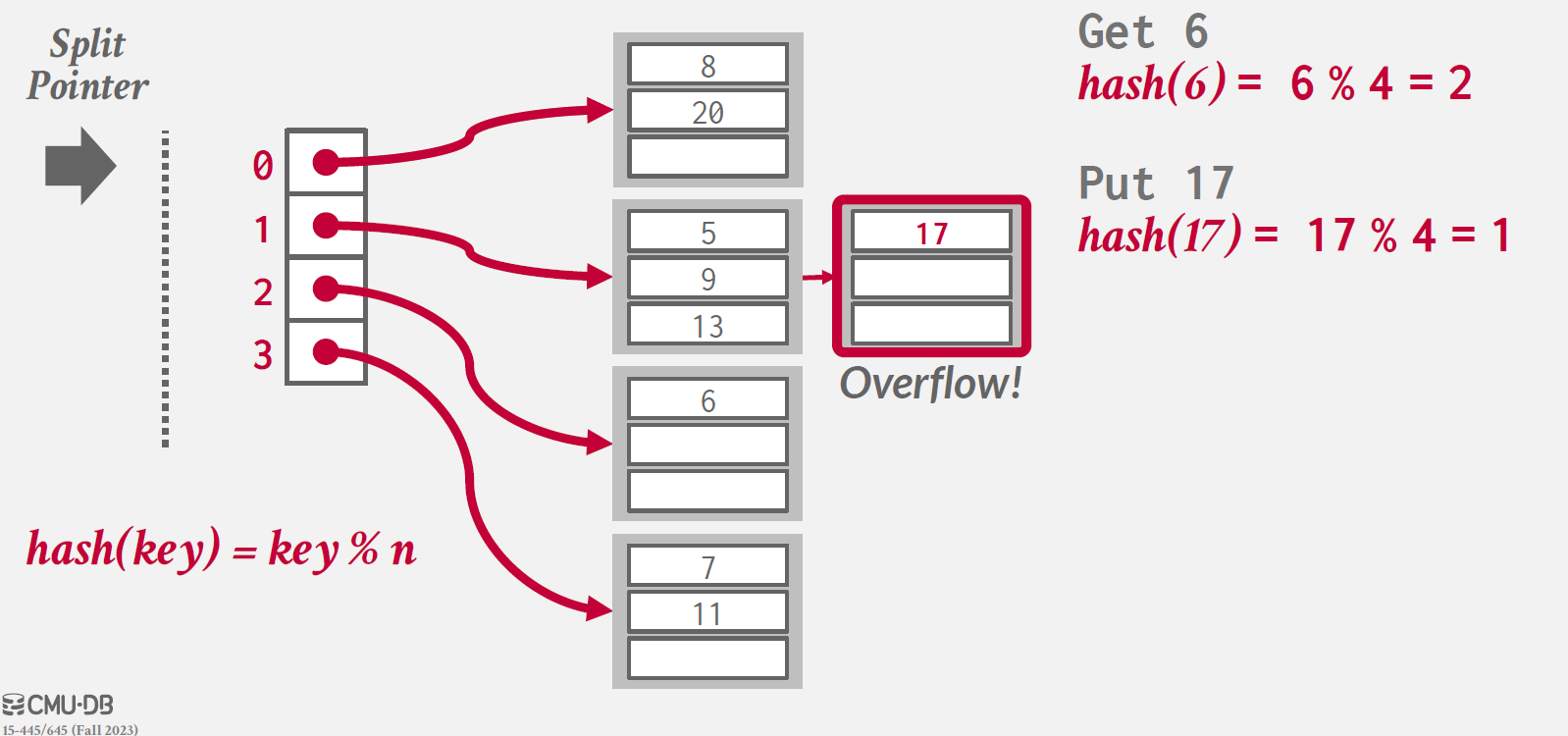
이 때, split pointer가 0번째 index를 가리키고 있기 때문에, 해당 bucket을 대상으로 split을 진행한다.
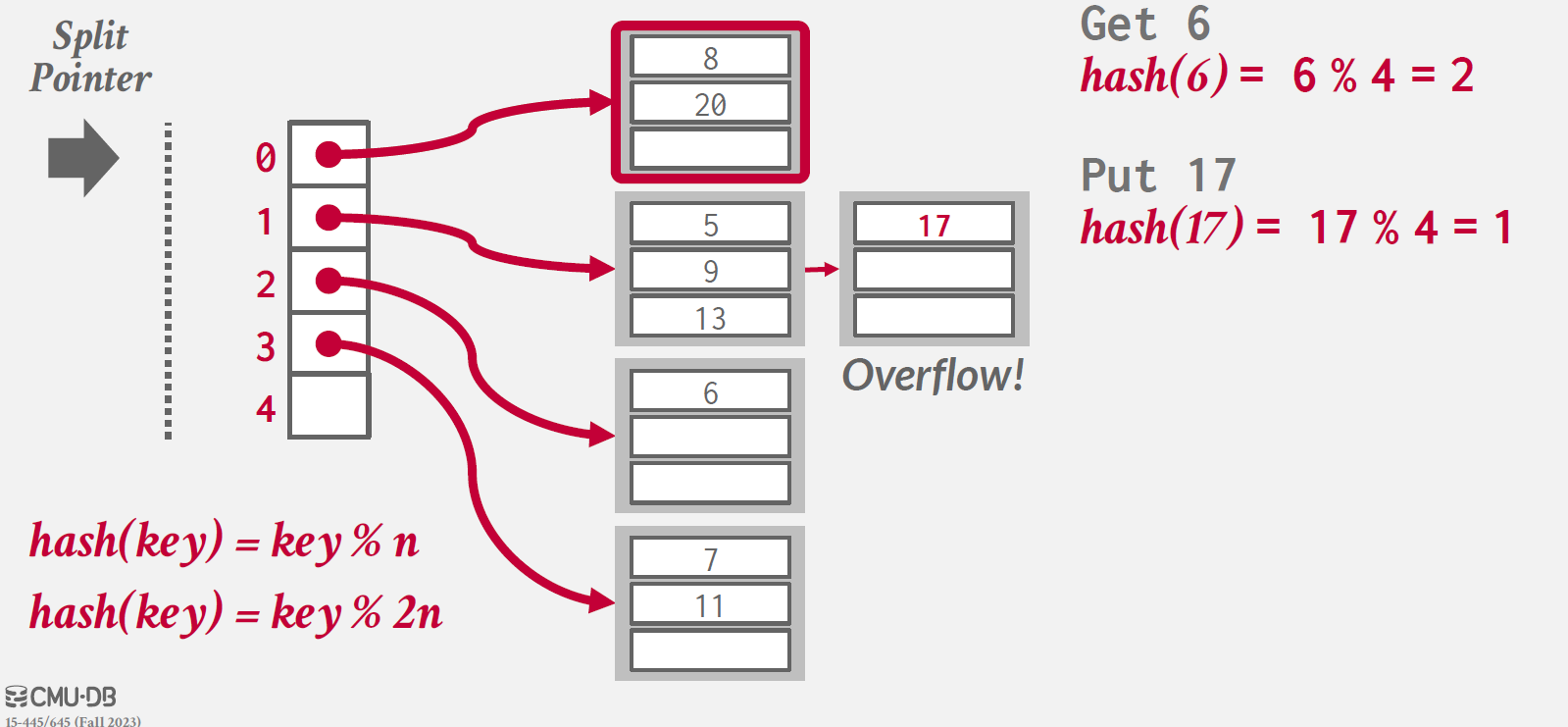
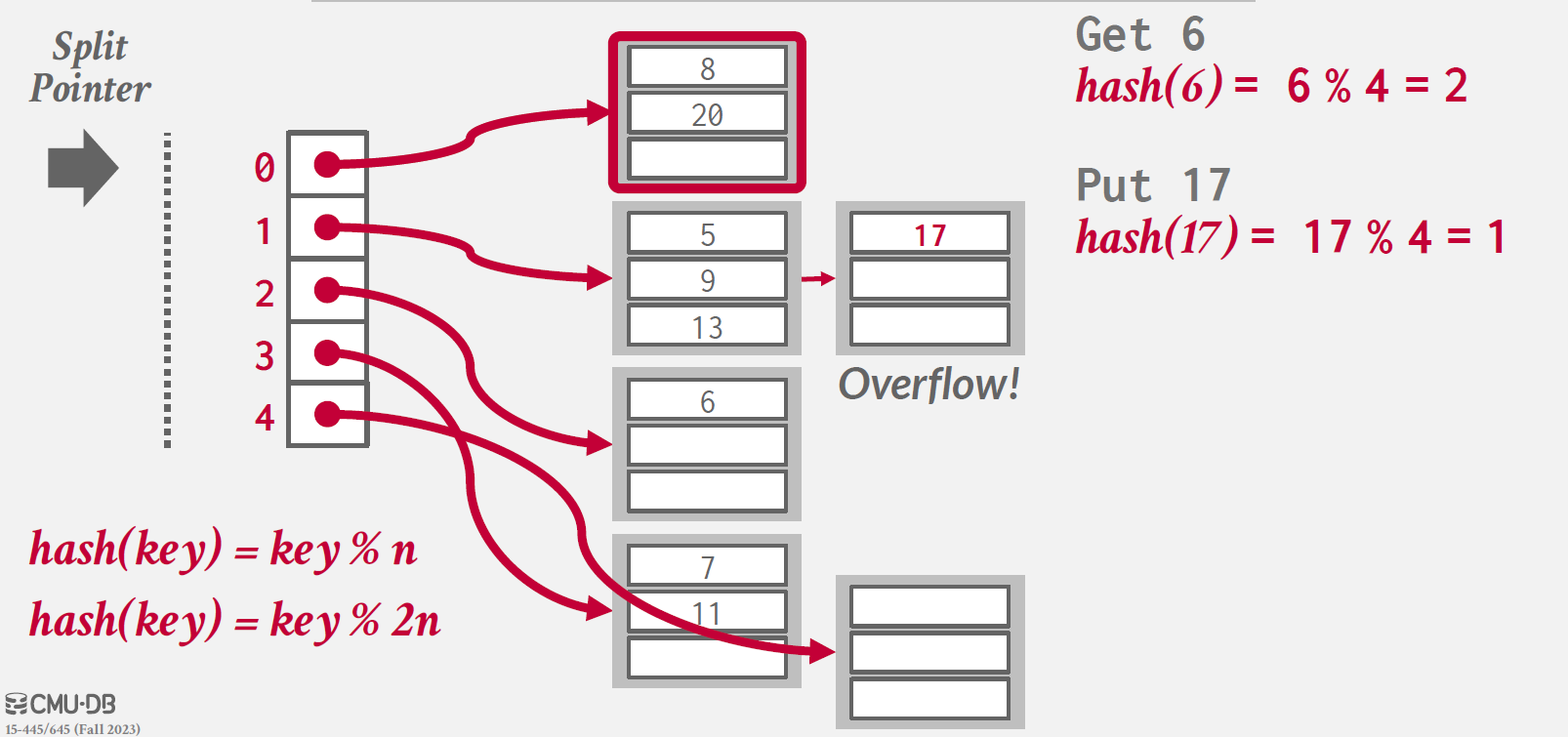
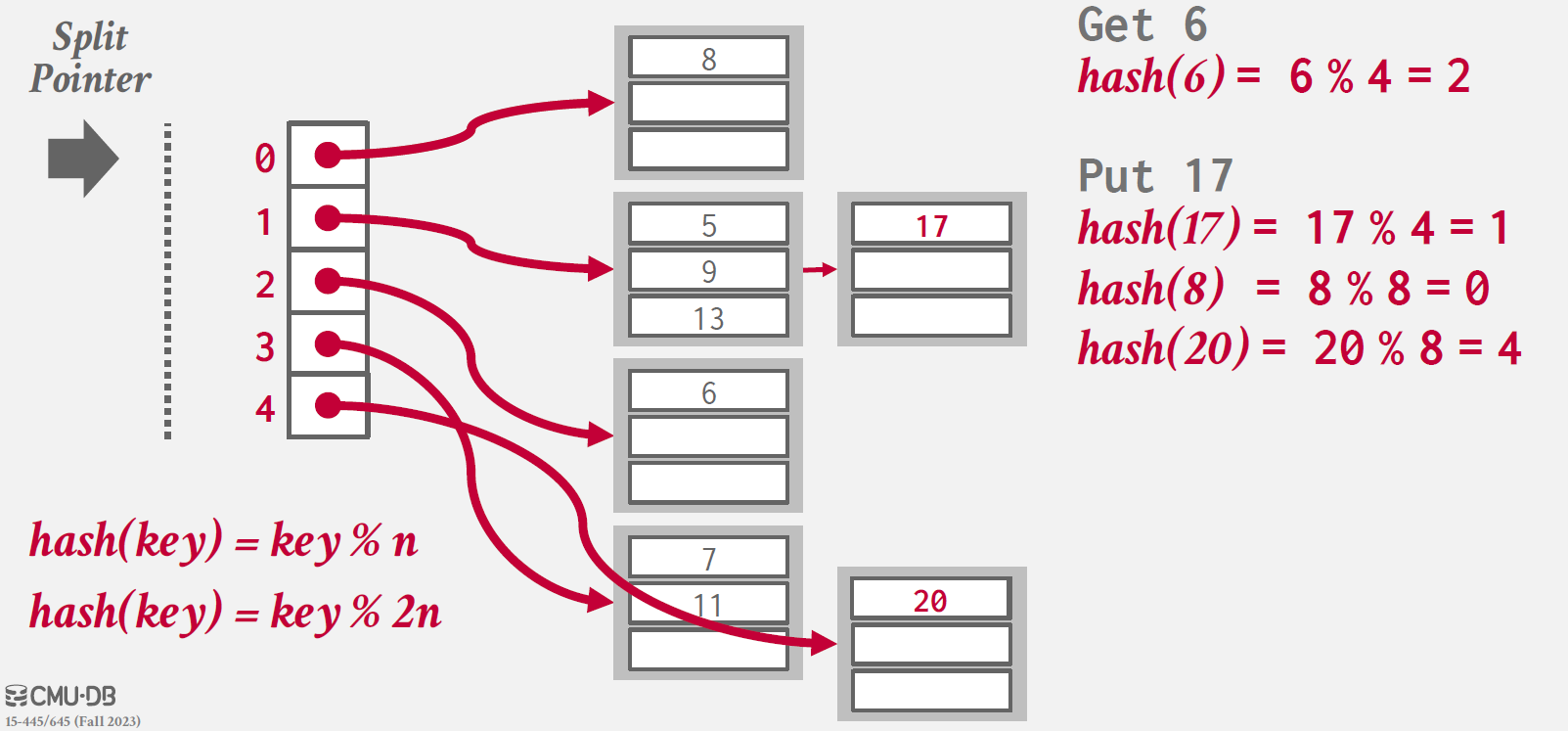
기존 entry에 대하여 새로운 hash 함수 (key % 2n)을 적용하여 split 대상 bucket에 있는 entry 대상으로 적용하고,
이동시킨다.
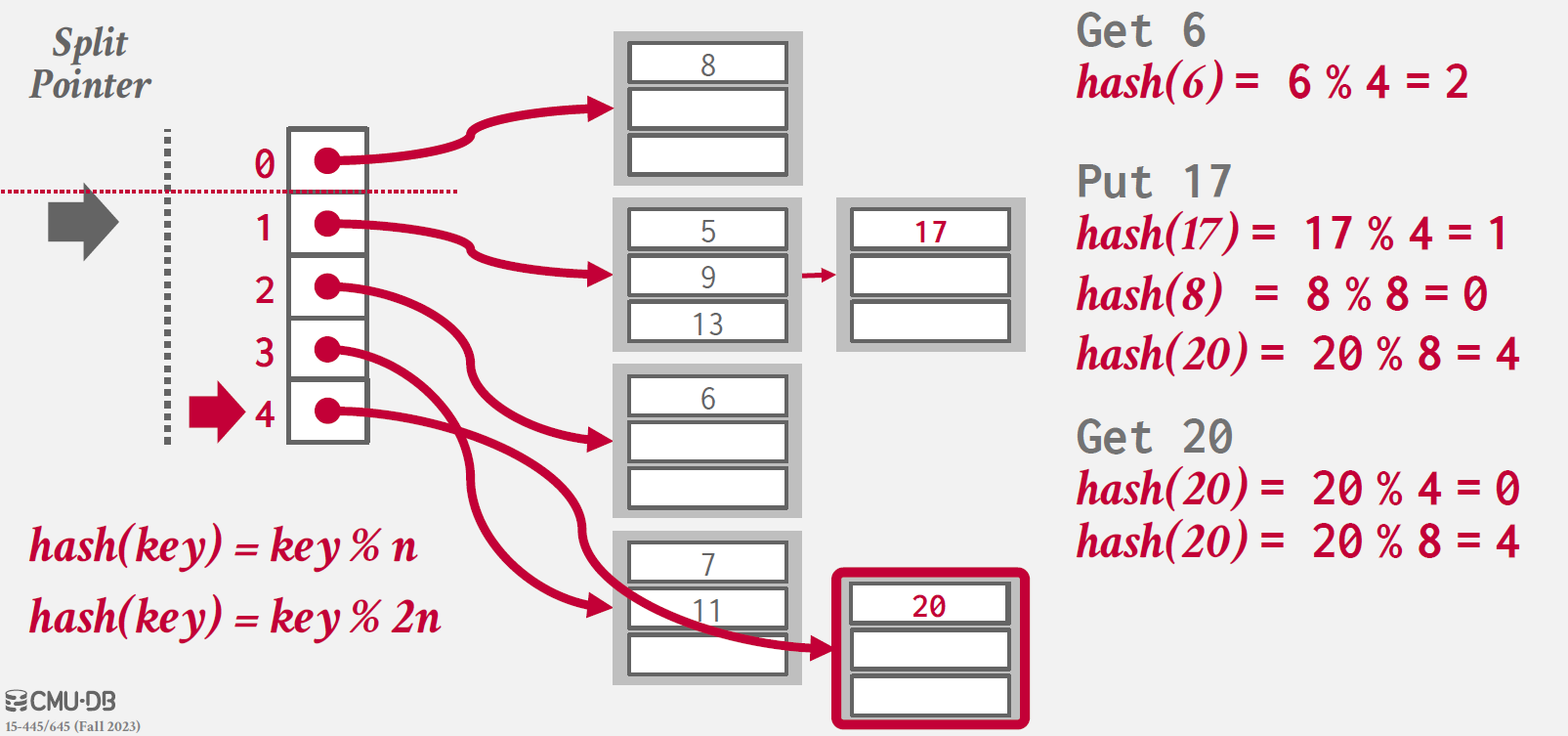
split 이후 hash 함수의 종류는 2개가 되었고, Get 20 요청을 처리하기 위해 두 번의 해싱을 진행한다.
이런식으로 반복하다보면, 0~3(기존에 이미 있었던 index)에 대해 언젠간 모두 split이 진행될 것이다.
이 경우 첫 번째 해쉬 함수(예제에서는 key % n)을 제거하고 두 번째 해쉬 함수만을 채택하여 hashing이 진행되며, split pointer는 첫 번째 인덱스의 위치로 이동한다.
만약 split pointer 아래에 있는 highest bucket이 비어있는 경우, hash table은 해당 bucket을 삭제하고 split pointer를 반대 방향으로 이동시킬 수 있다.
예시를 확인할 수 있는 Delete 과정은 다음과 같다.
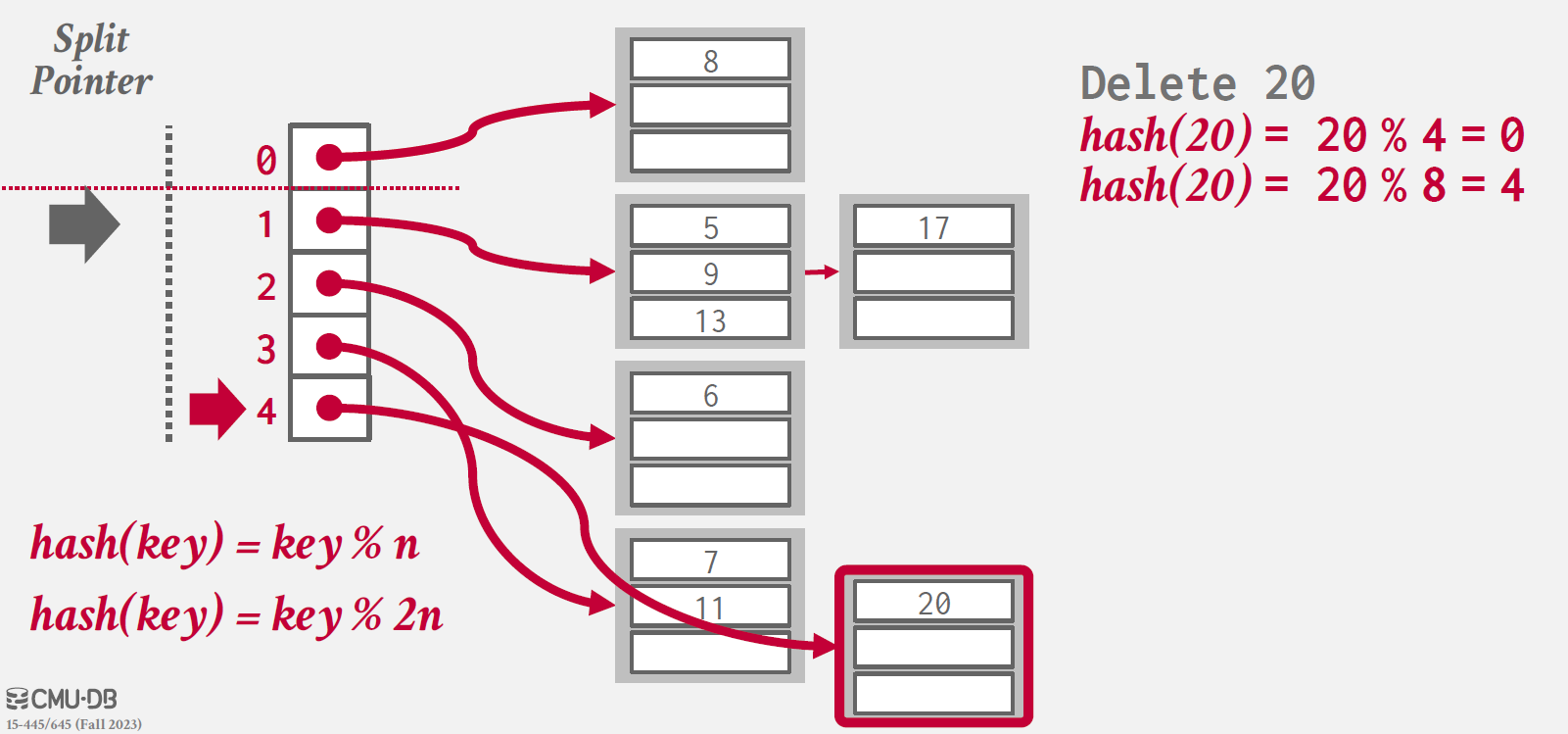
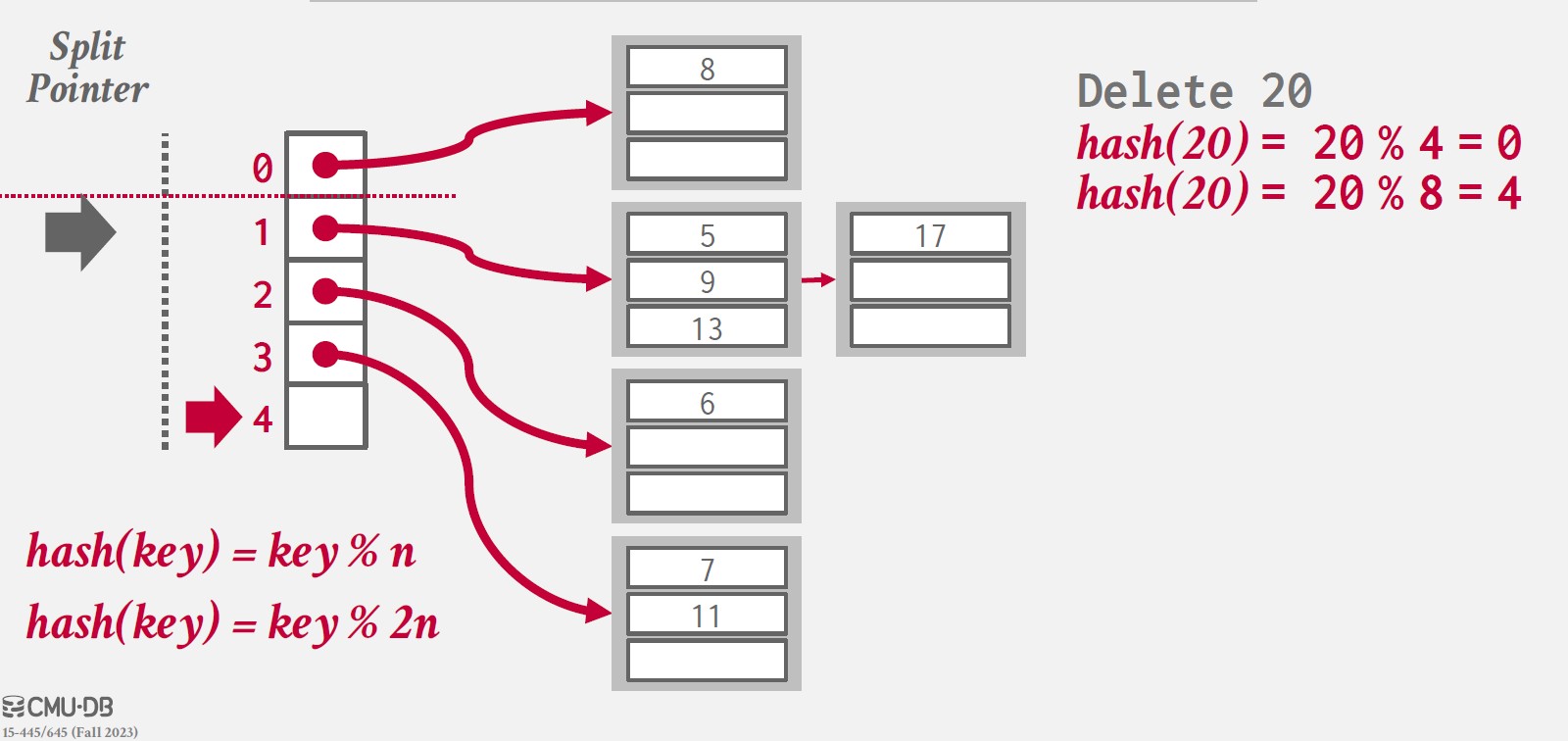
20을 삭제하면, 더 이상 index 4가 가리키는 bucket에 entry가 존재하지 않고, 따라서 해당 bucket을 제거한다.
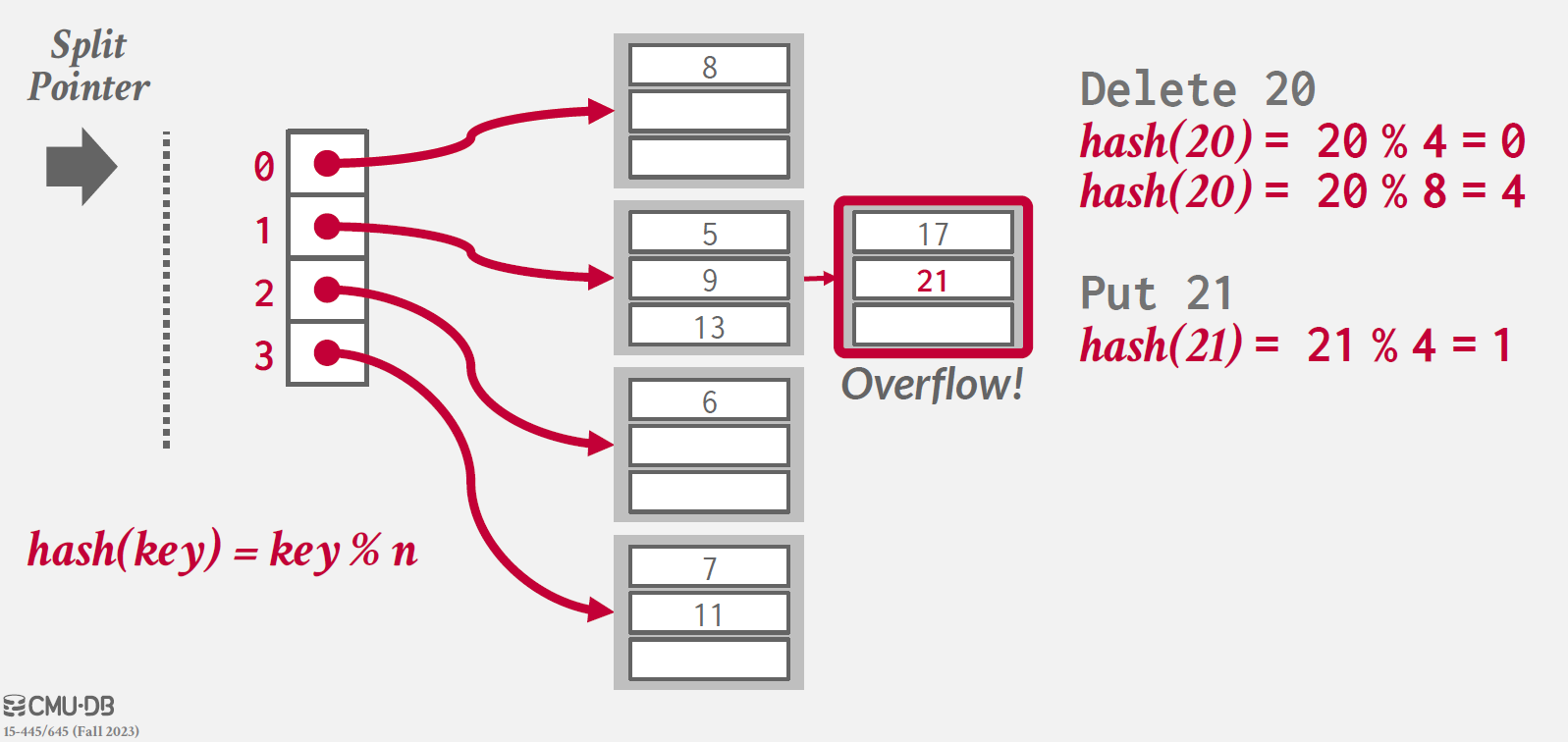
따라서 split pointer를 맨 처음으로 옮기고, 두 번째 hash 함수를 제거한다.
'DB' 카테고리의 다른 글
| [Database System] Join Algorithm (0) | 2023.10.15 |
|---|---|
| [Database System] B+ Tree Index (0) | 2023.10.12 |
| [Database System] Database Storage2 (0) | 2023.10.07 |
| [Database System] Database Storage (0) | 2023.10.05 |
| [Database System] Normalization (0) | 2023.10.05 |
![[Database System] Hash Table](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FZTvHt%2FbtsxrVTv3UD%2FAAAAAAAAAAAAAAAAAAAAAJPCMLqGBSSysWU9yMAtQOrmd1l-l9Ig0e58fujeFufy%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DAffpN5uW9xZIuuBZyAJCbAjWegM%253D)